
counter-clockwise) will result in tallying up to a successive or preceding number to the initial Fibonacci number counted in the clock-wise direction.

On the other hand, counting the number of seed spirals in the opposite direction (e.g. clock-wise), they will arrive at a number found in the Fibonacci sequence. One will often discover that when counting the seed spirals of a sunflower in one direction (e.g. A more renowned example can be identified in the beloved sunflower. Several species of plants, in which the exact number of flower petals are always found to one that is found in the Fibonacci sequence. The most famous examples are found in nature. Many of the real world illustrations of the Fibonacci sequence portray what most would consider beauty. So returning back to our example of the “golden rectangle”, what we would actually ascertain is that the ratio of its dimensions are 1:1.618.īeauty in the eye of the Fibonacci Sequence Earlier on in the sequence, the ratio approaches 1.618, but is particularly more evident later in the sequence as the numbers grow larger and larger, the ratio between two consecutive numbers approaches a near perfect 1:1.618 ratio. This value is originally derived from the ratio of two consecutive numbers in the Fibonacci sequence. So what exactly is so grand and “Golden” about these shapes? Unsurprisingly, the astounding property of these shapes stems from their “Golden ratios” – 1:1.618. Each number indicates the dimensions of the square it is in Adapted from Dicklyon Golden Rectangle with the first few terms from the Fibonacci sequence. triangles) and real world entities, as we shall soon discover. The Fibonacci spiral however is not limited to rectangles (although this is the most common shape used to depict the Fibonacci spiral) and can be found in a multitude of geometric shapes (e.g.
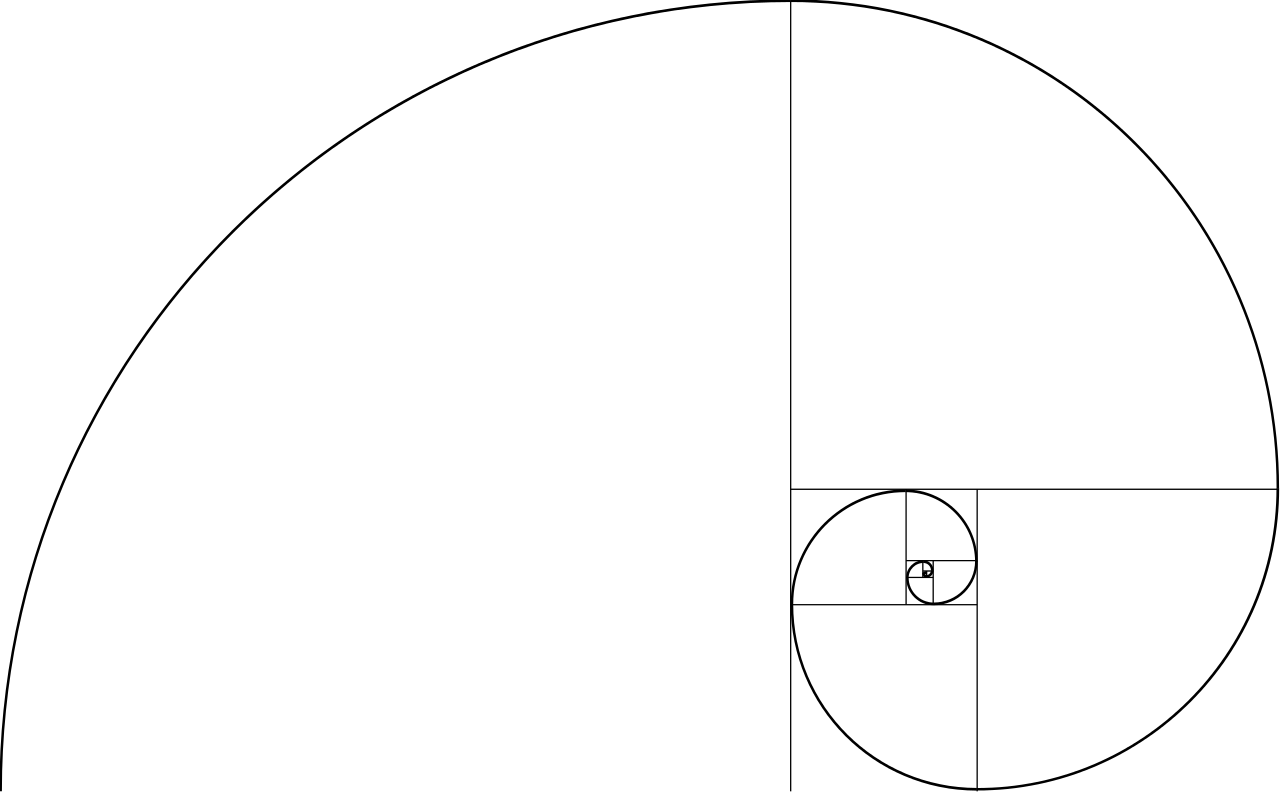
All together these squares are fitted perfectly within what is known as a “golden rectangle”. What appears to be an ordinary spiral forms unique quarter circles over each square that increases in size in according to the Fibonacci sequence. Now where exactly have we observed this sequence of numbers over and over again in our everyday life? Not quite in numeric form as you might have guessed….Īlso known as “the Golden Spiral”, in it’s most rudimentary form is outlined over a collection of squares that bear the dimensions of the Fibonacci sequence (1 x 1, 2 x 2, etc. In the Fibonacci sequence, each number can be derived from the sum of the two preceding numbers. One particular sequence that has garnered a strong reputation in it’s utility and ubiquity is the Fibonacci sequence. Not all mathematical sequences are easily separated into these two branches but are still incredibly interesting and applicable. For example, consider the half-life of a radioactive element – the common ratio is 2, and in a fixed amount of time, radioactive decay disintegrates the element by half. Geometric sequences on the other hand encompass a succession of numbers that share a common ratio between them. A familiar example would encompass the sequence of house numbers along a street you happen to drive by (e.g. Arithmetic sequences are defined by a string of consecutive numbers that have a common difference between them. You probably began differentiating between these two types of sequences while completing grade 11 math. arithmetic progression) and geometrics sequences (i.e. Patterns within mathematical sequences provide the key that reveals a common thread of how each number is connected to one another.īroadly speaking, mathematical sequences can be categorized into two major groups: arithmetic sequences (i.e. Each number within a mathematical sequence is identified as a term. Simply described, a math sequence is a group of numbers that follow a specific pattern. A more relevant memory today might be one of you reciting your times table. One’s earliest recollection of a math sequence probably began at the age of two, when you started counting to ten.

Math sequences can be discovered in your everyday life.


 0 kommentar(er)
0 kommentar(er)
